`Photoquantigraphy' with AGC: Joint parameter estimation in both
domain and range of functions in same orbit of the
projective-wyckoff group
Steve Mann
MIT Building E15-383, 20 Ames Street, Cambridge, MA 02139
Author currently with University of Toronto, Dept. Electrical
and Computer Engineering
10 King's College Road, Toronto, Ontario, M5S 3G4
Tel. (416) 946-3387; Fax. (416) 971-2326
mann@eecg.toronto.edu
http://www.wearcam.org
http://wearcomp.org
http://genesis.eecg.toronto.edu
http://www.eecg.toronto.edu/~/mann
October 1995
Also appears in:
@techreport{mann384,
author = "Steve Mann",
title = "JOINT PARAMETER ESTIMATION IN BOTH DOMAIN AND RANGE
OF FUNCTIONS IN SAME ORBIT OF THE
PROJECTIVE-{W}YCKOFF GROUP",
number = "384",
institution = "MIT Media Lab",
address = "Cambridge, Massachusetts",
month = "December",
year = "1994",
note = "also appears in:
Proceedings of the
IEEE International Conference on Image Processing (ICIP--96),
Lausanne, Switzerland, September 16--19, 1996,
pages 193--196"
}
A PostScript version of this paper is also available.
Abstract:
Consider a static scene and fixed center
of projection, about which a camera is free to zoom, pan, tilt, and rotate
about its optical axis. With an ideal camera,
the resulting images are in the same orbit of the projective group-action,
and each pixel of each image provides a measurement of
a ray of light passing through a common point in space.
Unfortunately, most modern cameras have a built in
automatic gain control (AGC), automatic shutter, or auto-iris, which, in
many cases cannot be turned off.
Many modern digitizers to which cameras are connected have their
own AGC which also cannot be disabled.
With AGC, the characteristic response function of the camera varies,
making it impossible to accurately describe one image as a projective
coordinate transformed version of another.
This paper proposes not only a solution to this problem, but
a means of turning AGC into an asset, so that
even in cases where AGC could be disabled, photoquantigraphers of the future
will be turning AGC on.
Suppose we take two pictures, using the same settings
(in manual exposure mode), of the same
scene, from a fixed common location (e.g. where the camera is free to zoom,
pan, tilt, and rotate about its optical axis
between taking the two pictures). Both of the
pictures capture the same pencil of light
, but each one projects this information differently onto
the film or image sensor. Neglecting that which falls beyond the
borders of the pictures, the images are in the same orbit of the
projective group of coordinate transformations.
The use of projective (homographic) coordinate transformations to
automatically (without use of explicit features) combine
multiple pictures of the same scene into a single picture of greater
resolution or spatial extent, was first described in 1993[1].
These coordinate transformations were shown to capture the
essence of a camera at a fixed center of projection (COP) in a static
scene.
Note that the projective group of coordinate transformations
is not Abelian and there is thus
some uncertainty in the estimation of the parameters
associated with this group of coordinate transformations[2].
However, we may first estimate parameters of Abelian subgroups
(for example, the pan/tilt parameters, perhaps
approximating them as a 2-D translation so that
Fourier methods[3] may be used).
Estimation of zoom (scale) together with pan and tilt, would incorporate
non-commutative parameters (zoom and translation don't commute), but could
still be done using the multiresolution Fourier
transform[4][5], at least as a first step,
followed by an iterative paramter estimation procedure over all parameters.
An iterative approach to the estimation of the parameters
of a projective (homographic) coordinate transformation between images
was suggested in[1], and later in [6]
and [7].
Lie algebra is the algebra of symmetry, and pertains to the behaviour of
a group in the neighbourhood of its identity. With typical video
sequences, coordinate transformations
relating adjacent frames of the sequence are very close to
the identity. Thus we may use the Lie algebra of the group when
considering adjacent frames of the sequence, and then use the group
itself when combining these frames together. Thus, for example, to
find the coordinate transformation, 
, between 
, Frame 0
and 
, Frame 9,
we might use the Lie algebra to estimate
(the coordinate transformation between
Frame 10 and 11) and then estimate 
between frames 
and 
,
and so on, each one being found in the neighbourhood of the identity.
Then to obtain , we use the true law of composition of the
group: 
.
An ideal spotmeter
is a perfectly directional lightmeter which measures the quantity
of light, q, arriving from the direction in which it is pointed.
The direction in which it is pointed may be specified in terms
of its azimuth, 
, and its elevation, 
.
The `photoquantigraph'
is a recording of the pencil of light rays
passing through a given point in
space, and could, in principle, be measured with a dense array of
spotmeters aimed toward that point.
(Fig 1).
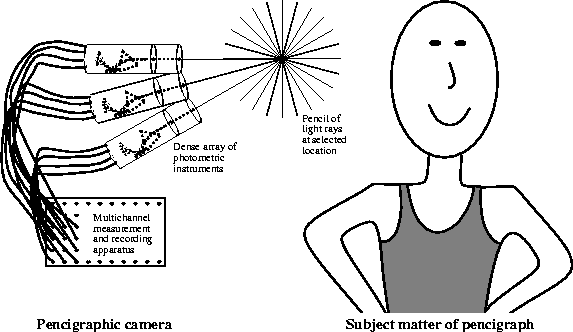
Figure: The `photoquantigraph'
is a recording of the pencil of light rays
passing through a given point in space. Such a recording could
be approximated by a discrete array of spotmeters, angled
toward a common point -- the center of projection.
Panoramic photography attempts to record a large portion of the `nonmetric
photoquantigraph'
onto a single piece of film (often by rotating
the camera while sliding the film through a slit).
The nonmetric photoquantigraph may also be estimated from a collection of pictures
all taken from the same point in space (with differing camera orientations and
lens focal lengths).
The basic philosophy is that the camera may
be regarded as an array of (nonmetric) spotmeters, measuring rays of light
passing through the COP.
To each pair of pixel indices
of the sensor array in a camera, we may associate
an azimuth and elevation.
Eliminating lens distortion[8] makes the images
obey the laws of projective geometry, so that they are (to within
image noise and cropping) in the same orbit of the projective group action.
(Lens distortion may also be simply absorbed into the mapping between pixel
locations and directions of arrival.)
Trying to use a pixel from a camera as a lightmeter raises many
interesting and important problems.
The output of a typical camera, f, is not linear with respect to the
incoming quantity of light, q. For a digital camera,
the output, f, is the pixel value, while for film, the output might
be the density of the film at the particular location under consideration.
I will assume that the output is some unknown but
monotonic function of the input. Monotonicity,
a weaker constraint than linearity, is what I
mean by ``nonmetric spotmeter'' -- our knowledge of the quantity of
light received is in terms of the nonmetric quantity f(q), not q itself.
Models for the nonlinearity, f, include
the classic response curve[9]:
or the author's 
curve that attempts to capture the toe and shoulder regions of the
response.
Methods to estimate the unknown response curve from pictures that differ only
in exposure, have also
been proposed[10]. These methods are based on computing the
joint histogram between differently exposed pictures, and then estimating
the function g(f), defined by
where q(x,y) is the quantity of light received in a first exposure,
and kq(x,y), the quantity of light received in a second exposure,
is k times that of the first exposure. In traditional film cameras,
k would most likely be 
, but in electronic cameras,
k may vary continuously.
Since the response curve, f, is assumed to be unknown, we begin with the
estimates of the
so-called `range-range'[10] plots, g(f(q)) = f(kq)
versus f(q)
(so-called because they represent the range of the response curve
plotted against the range of the response curve for a different exposure).
Examples of the range-range plots for various values of k, appear
in Fig 2. (These plots completely
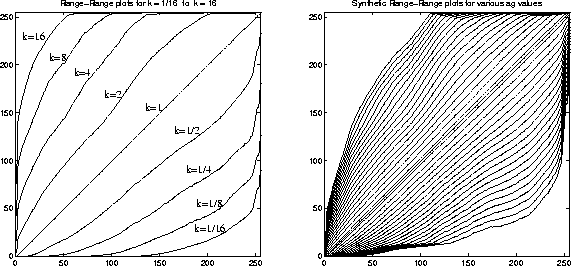
Figure: Range-range plots, g(f(q(x,y))) = f(kq(x,y)),
characterizing the specific camera and
digitizer combination used by author.
(a) plots estimated from joint histograms
of differently exposed pictures of the same scene.
(b) family of curves generated by the `exact' model,
for various values of the input parameter.
characterize the response of a specific camera and digitizer -- a system
designed and built by the author, comprising a miniature camera built
into a pair of eyeglasses together with a tiny computer screen, connected
to clothing containing a digitizer with Internet connection; further
information is available from the Web site listed in the titlepage.)
If what is desired is a picture of increased spatial extent
or spatial resolution, the nonlinearity is not a problem, so long as it is not
image dependent. However, most low-cost cameras have a built in automatic
gain control (AGC), electronic level control, auto iris, or some other form of
automatic exposure
which cannot be turned off or disabled.
This means that the unknown response function, f(q), is image dependent,
and will therefore change over time, as the camera framing changes to
include brighter or darker objects.
Although AGC was a good invention for its intended application
(serving the interests of most camera users
who merely wish to have a properly exposed picture without having to make
adjustments to the camera), it has previously thwarted attempts to estimate
the projective coordinate transformation between frame pairs.
Examples of an image sequence, acquired using a camera with AGC, appear
in Fig 3.
Figure: The `fire-exit' sequence, taken using a camera with AGC.
(a)-(j) frames 1-10 of the sequence:
as the camera pans across to take in more of the
open doorway, the image brightens up showing more of the
interior, while, at the same time, clipping highlight detail.
Frame 10 (a) shows the writing on the white paper taped to the
door very clearly, but the interior is completely black.
In frame 13 (d) and beyond, the paper is completely obliterated,
but more and more detail of the interior becomes visible,
showing that the fire exit is blocked by the clutter inside.
(k)-(t) `certainty' images corresponding to (a)-(j).
The purpose of this paper is to propose a joint estimation of the
projective coordinate transformation and the tone-scale change.
Each of these two may be regarded as a ``motion estimation'' problem
if we extend the concept of ``motion estimation'' to include both
`domain motion' (motion in the traditional sense) as well as
`range motion' (Fig 4).
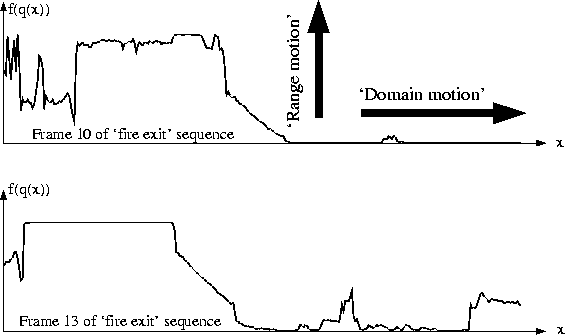
Figure:
Center rasters of two images from the `fire exit' sequence.
`Domain motion' is motion in the traditional sense
(e.g. motion from left to right, zoom, etc.), while
`Range motion' refers to a tone-scale adjustment
(e.g. lightening or darkening of the image).
In this case, the camera is panning to the right,
so domain motion is to the left. However, when panning
to the right, the camera points more and more into the darkness
of an open doorway, causing the AGC to adjust the exposure.
Thus there is some ``upwards'' motion of the curve as well
as ``leftwards'' motion. Just as panning the camera
across causes information to leave the
frame at the left, and new information to enter at the right,
the AGC causes information to leave from the top (highlights
get clipped)
and new information to enter from the bottom (increased
shadow detail).
As in[6], we consider one dimensional ``images'' for
purposes of illustration, with the understanding that the actual
operations are performed on 2-D images.
The 1-D projective-Wyckoff group is defined in terms of the group
of projective coordinate transformations, taken together with the
one-parameter group of image darkening/lightening operations:
where g characterizes the lightening/darkening operation.
The law of composition is defined as:
where the first law of composition on the right hand side is the usual
one for the projective group, and the second one is that of the
one-parameter lightening/darkening subgroup.
Two successive frames of a video sequence are related through a group-action
that is near the identity of the group, thus one may think of the Lie
algebra of the group as providing the structure locally.
As in previous work[6] an approximate model
which matches the `exact' model in the neighbourhood of the identity is used.
For the projective group, the approximate model
has the form 
.
For the `Wyckoff group' (which is a one parameter group isomorphic to
addition over the reals, or multiplication over the positive reals),
the approximate model may be taken from Eq 1, by noting
that
This equation suggests that linear regression on the joint histogram between
two images would provide an estimate of 
and 
, while
leaving 
unknown, which is consistent the fact that the response
curve may only be determined up to a constant scale factor.
From (4)
we have that the (generalized) brightness change constraint equation is
.
Combining this equation with the Taylor series
representation 
,
the equation of motion becomes:
.
Minimizing 
yields a linear solution in substituted variables (that are easily
related to the variables of the approximate model):
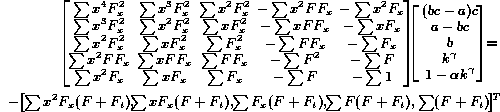
where F(x,t)=f(q(x)) at time t, 
, at time t,
and 
is the frame difference of adjacent frames.
To construct a single floating-point image of increased spatial
extent and increased dynamic range,
each pixel of the output image is constructed
from a weighted sum of the images whose coordinate-transformed bounding
boxes fall within that pixel. The weights in the weighted sum are the
so-called `certainty functions'[10], which are found by
evaluating the derivative of the
corresponding `effective response function' at the
pixel value in question. While the response function, f(q),
is fixed for a given camera, the `effective response function',
depends on the exposure, 
, associated with frame, i,
in the image sequence. By evaluating 
, we arrive
at the so-called `certainty images' (Fig 3).
Lighter areas of the `certainty images' indicate moderate values of
exposure (mid-tones in the corresponding images), while darker values
of the certainty images designate exposure extrema -- exposure in the
toe or shoulder regions of the response curve
where it is difficult to discern subtle differences in exposure.
The photoquantigraphic estimate may be explored interactively on a computer
system (Fig 5), but
the simultaneous wide dynamic range and ability to discern subtle differences
in greyscale are lost once the image is reduced to a tangible form (e.g.
a hardcopy printout).
Figure: Floating point photoquantigraphic image constructed from the
fire-exit sequence. The dynamic range of the image is far
greater than that of a computer screen or printed page.
The photoquantigraphic information
may be interactively viewed on the computer screen, however,
not only as an environment map (with pan, tilt, and zoom),
but also with control of `exposure' and contrast.
With a `virtual camera' we may move around in the photoquantigraph,
both spatially and tonally.
In order to print a picture of such dynamic range it may be preferable to
relax the monotonicity constraint, and perform some local tone-scale
adjustments (Fig 6).
Figure: Fixed-point image made by
tone-scale adjustments that are only locally monotonic,
followed by quantization to 256 greylevels.
Note that we can see clearly both the small piece of white paper on
the door (and even
read what it says -- ``COFFEE HOUSE ''),
as well as the details of the dark interior.
Even if the end goal is a picture of limited dynamic
range (as in Fig 5),
perhaps where the artist wishes to deliberately wash out highlights
and mute down shadows for expressive purposes, the author's philosophy
is that one should attempt to capture as much information about the
scene as possible, produce a photoquantigraphic estimate, and then ``put expression''
into that estimate (by throwing away information in a controlled
fashion) to produce a final picture.
The procedure for self-calibrating a camera (to within a constant
scale factor) has been exploited for capturing photoquantigraphic measurements,
in particular, treating the camera as an array of photometric measuring
instruments. This has been accomplished by proposing
and implementing a global motion estimation
algorithm which considers jointly global
``motion'' in the domain and range of
the functions undergoing ``motion''.
Dynamic range has been extended by combining differently exposed images
where the AGC, rather than thwarting motion estimation algorithms as
is generally otherwise the case, actually provides both
more information
from the scene and information about the camera's unknown response function.
Thanks to Rosalind Picard, Charles Wyckoff, Shawn Becker, and
Berthold Horn for
many interesting discussions.
References
- 1
-
S. Mann.
Compositing multiple pictures of the same scene.
In Proceedings of the 46th Annual IS&T Conference,
Cambridge, Massachusetts, May 9-14 1993. The Society of Imaging Science and
Technology.
- 2
-
S. Mann and R. W. Picard.
Video orbits of the projective group; a simple approach to
featureless estimation of parameters.
TR 338, Massachusetts Institute of Technology, Cambridge, Ma, See
http://n1nlf-1.eecg.toronto.edu/tip.ps.gz 1995.
Also appears IEEE Trans. Image Proc., Sept 1997, Vol. 6 No. 9.
- 3
-
Bernd Girod and David Kuo.
Direct estimation of displacement histograms.
OSA Meeting on IMAGE UNDERSTANDING AND MACHINE VISION, June
1989.
- 4
-
R. Wilson, A. D. Calway, E. R. S. Pearson, and A. R. Davies.
An introduction to the multiresolution Fourier transform.
Technical report, Department of Computer Science, University of
Warwick, Coventry CV4 7AL UK., 1992.
ftp://ftp.dcs.warwick.ac.uk/reports/rr-204/.
- 5
-
A D Calway, H Knutsson, and R Wilson.
Multiresolution estimation of 2-d disparity using a frequency domain
approach.
pages 227-236. Springer-Verlag, September 1992.
- 6
-
S. Mann and R. W. Picard.
Virtual bellows: constructing high-quality images from video.
In Proceedings of the IEEE first international conference on
image processing, Austin, Texas, Nov. 13-16 1994.
- 7
-
R. Szeliski and J. Coughlan.
Hierarchical spline-based image registration.
CVPR, pages 194-201, 1994.
- 8
-
Lee Campbell and Aaron Bobick.
Correcting for radial lens distortion: A simple implementation.
TR 322, M.I.T. Media Lab Perceptual Computing Section, Cambridge, Ma,
Apr 1995.
- 9
-
Charles W. Wyckoff.
An experimental extended response film.
S.P.I.E. NEWSLETTER, JUNE-JULY 1962.
- 10
-
S. Mann and R.W. Picard.
Being `undigital' with digital cameras: Extending dynamic range by
combining differently exposed pictures.
Technical Report 323, M.I.T. Media Lab Perceptual Computing Section,
Boston, Massachusetts, 1994.
Also appears, IS&T's 48th annual conference, pages 422-428, May
1995.
`Photoquantigraphy' with AGC: Joint parameter estimation in both
domain and range of functions in same orbit of the
projective-wyckoff group
This document was generated using the LaTeX2HTML translator Version 96.1-h (September 30, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 icip96.
The translation was initiated by Steve Mann on Sun Jan 4 21:51:20 EST 1998
- ...group
- This work sponsored in part by Hewlett-Packard Research Labs.
- ...light
- We neglect the
boundaries of the sensor array and assume that both pictures
have sufficient field of view to capture all of the objects of
interest.
- ...`photoquantigraph'
- Terminology in single quotes is that
defined by the author here or elsewhere.
- ...photoquantigraph'
- By nonmetric, I mean that
even if we know the exact direction of arrival
corresponding to each pixel in the panoramic picture,
it does not tell us the actual quantity of light
arriving from that direction.
- ...exposure
- I refer to all of these methods of automatic
exposure control as AGC, whether or not they
are actually
implemented using gain.
Steve Mann
Sun Jan 4 21:51:20 EST 1998